חישוב סטטי של מבנה הנבנה בשלבים

חישוב סטטי של מבנה הנבנה בשלבים - הרעיון לכתוב על נושא זה עלה בעקבות שני אירועים.

באירוע הראשון הגשתי חוות דעת מקצועית לבחינת שקיעה גדולה בסלון דירת בית מגורים, במבנה מדורג בחיפה, שהיה בשלבי בניה סופיים. השקיעה במרכז הסלון היתה בשיעור של כ 7.5 ס"מ וניתן היה לראותה ללא מדידה.

האירוע השני היה בעקבות שאלה שנשאלה על ידי אחד הגולשים באתר זה, לגבי תוכנה לחישוב חתך מרוכב מבטון ופרופיל פלדה, מתוך רצון לתכנן חיזוק של קורה, לצורך הריסת עמוד תומך במהלך שיפוץ.

לגבי האירוע הראשון, בדקתי את התכניות והחישובים הסטטיים מתוכם עלה כי רצפת הסלון נסמכה על עמוד מתיחה עליון שחובר לקורה בקומה מעל. יש לציין כי בתכניות הקונסטרוקטור הופיעה הערה ברורה כי "יש לתמוך את התקרה עד לאחר יציקת המפלס שמעליה". הערה זאת בעייתית מכיון שעם גמר היציקה של התקרה שמעל, בעוד הבטון הינו עיסתי, יכול הקבלן לפרק את טפסנות התקרה התחתונה, אשר טרם הגיעה לחוזקה הרצוי.

הדבר בעייתי במיוחד מאחר והתקרה התחתונה אמורה להיות תמוכה על ידי העמוד התלוי ותמיכה זאת אינה יכולה להתקבל, כך שהתקרה התחתונה, שטרם הגיעה לחוזקה המלא, עמוסה בעומס הקרוב לעומס השרות המכסימלי (משקל עצמי של שתי תקרות) וזאת ללא עמוד תמיכה דבר שיגרום בהכרח לשקיעות גדולות שאינן מתוכננות.

לגבי האירוע השני, ההתייחסות לסוג זה של עבודות שיפוץ בדרך כלל אינה יסודית ומעמיקה, למרות שמדובר בנושא בטיחותי מחד וברצון להוזיל את העבודה ככל שניתן מאידך. הגישה הרוווחת בסוג זה של חיזוק קורות בטון, היא לחשב על צד הביטחון ולמסור לפרופיל הפלדה את כל העמס ושהוא יהיה זה שיגשר על המפתח שיגדל. כמובן שכאן מדובר בבזבוז. אפשרות מקובלת אחרת היא לחשב את החתך המשולב של קורות בטון אליה צמוד פרופיל פלדה, כחתך מרוכב ובהתאם לחשב את המאמצים. אבל סוג זה של חישוב מתעלם מהמאמצים והשקיעות של קורת הבטון הקיימים כבר במצבה הקודם.

כמובן שהפתרון נמצא בין שתי הגישות לעיל. בשלב הראשון נבנה המבנה המקורי וקורת הבטון שקעה בהתאם לעומסים והסכימה הסטטית. במהלך הצמדת פרופיל הפלדה לקורה הוא אינו נושא מאמצים כלל. פירוק העמוד התומך יגרום לשקיעה משותפת של הקורה המרוכבת. חישוב לדוגמא אבצע בהמשך המאמר.

בדרך כלל כשמתכננים מבנה, אזי לצורך קביעה של הסכימה הסטטית ומצב העומסים ולחישוב הכוחות הפנימיים והשקיעות, מתייחסים למבנה במצבו הסופי. בפועל המצב שונה, מבנה נבנה בדרך כלל בשלבים, כאשר בכל שלב נוצרים שקיעות, משתנים העומסים, ואפילו חוזק האלמנטים משתנה עם הזמן. בדרך כלל ההשפעה של חישוב מבנה הנבנה בשלבים, לעומת חישוב המבנה במצבו הסופי היא שולית וההבדלים בין הגישות אינה משמעותית. אולם, ישנם מצבים, בהם קיים הבדל משמעותי בין שתי הגישות. כמו למשל, בסכימה סטטית של עמודים ה"צומחים" מקורות, או עמודים העובדים במתיחה ומעבירים עומסים לקורה שמעליהם וכד`.

לשם המחשה, נניח מצב של יציקת קומה ראשונה. לאחר מספר ימים מפרקים את הטפסות והרצפה מתחילה לשקוע תוך קבלת כוחות פנימיים לנשיאת עומסי המשקל העצמי של התקרה. בזמן זה הבטון כמובן טרם קיבל את חוזקו המקסימלי. לאחר מספר ימים נוסף יוצקים את תקרת הקומה הבאה כאשר משקל הבטון שנוצק מעמיס את הטפסות הנשענות על תקרת הקומה הראשונה. לאחר מספר ימים שוב מפרקים את הטפסות כאשר התקרה הראשונה כבר שקעה מעומסי המשקל העצמי של שתי התקרות וכך הלאה עד לגמר יציקת שלד המבנה.

בשלבים הבאים, לאחר ששלד המבנה נמצא במצבו הסופי, מעמיסים אותו בעומסים קבועים נוספים (ריצוף, מחיצות, טיח וכד`) ורק כשהמבנה גמור, מעמיסים אותו בעומסים השימושיים.
בחישוב סטטי לא ליניארי של בניה בשלבים (STAGED CONSTRUCTION) בכל שלב נלקחים בחשבון המצב ההתחלתי של השקיעות והכוחות הפנימיים של השלב הקודם ומבוצע חישוב באיטרציות רבות עד לקבלת שווי משקל סטטי של השלב הנוכחי.

לדוגמא ניקח מבנה מסגרת של 3 קומות עם עמוד ה"צומח" מקורת הקומה הראשונה.

עומסים הפועלים על הקורות הינם:

עומס קבוע (משקל עצמי של התקרות) = 2 טון למ"א
עומס קבוע (משקל עצמי של ריצוף , מחיצות טיח וכו`) = 1.4 טון למ"א
עומס שימושי = 0.6 טון למ"א

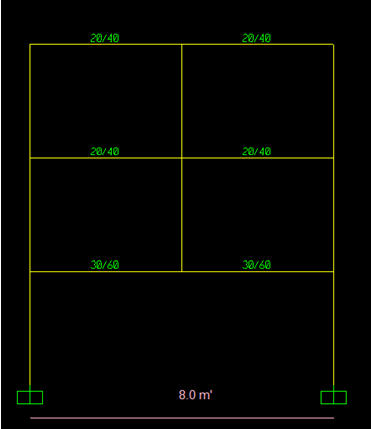
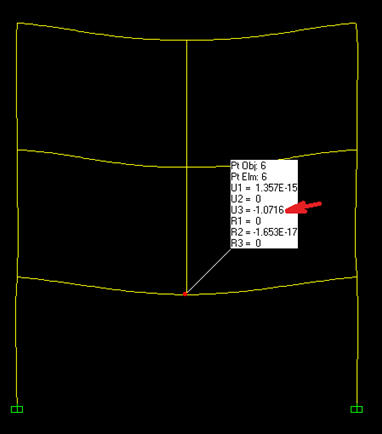
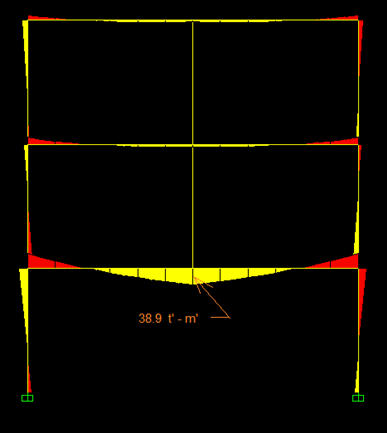
בתרשים הבא נראה את סכימת מבנה המסגרת המישורית עם מידות הקורות:

נחשב את המבנה במצבו הסופי עם העומסים הפועלים עליו ללא מקדמי הבטיחות (במצב שירות). בתרשימים הבאים נראה את השקיעות והמומנטים של המבנה במצבו הסופי. השקיעה המתקבלת במרכז הקורה הנושאת היא 1.07 ס"מ והמומנט הינו 38.9 טון - מטר.

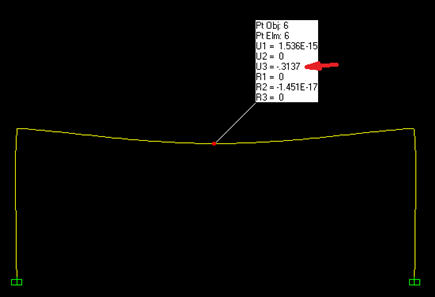
מכאן נעבור לחישוב הלא ליניארי של המבנה על שלבי הביצוע השונים. בשלב ראשון נעמיס את הקומה הראשונה בעומס הקבוע. בשלב זה נניח כי הבטון עדין לא הגיע לחוזק של ב-30 ונניח שהוא שווה ערך ל ב - 25. בתרשים נראה את מהלך השקיעות של מצב זה.

השקיעה במרכז הקורה היא קצת מעל 0.31 ס"מ. בשלב שני נעמיס את תקרת הקומה הראשונה בעומס הקבוע של התקרה השניה. בשלב שלישי נעמיס את תקרת הקומה השניה בעומס הקבוע ונחסר את העומס הזה מתקרת הקומה הראשונה. כאן נניח כי הבטון של קורת הקומה הראשונה כבר התחזק לרמה של ב-30.

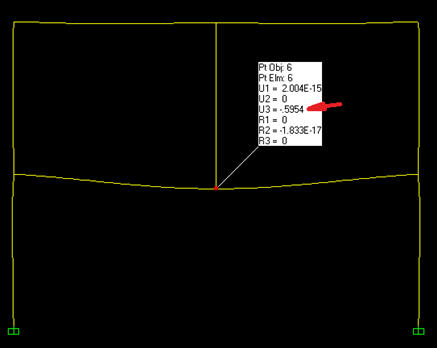
כאן נראה כי השקיעה כמעט 0.6 ס"מ. בשלב רביעי נעמיס את תקרת הקומה השניה בעומס הקבוע של תקרת הקומה השלישית. בשלב חמישי נעמיס את תקרת הקומה השלישית בעומס הקבוע ונחסר את עומס זה מתקרת הקומה השניה. בתרשים שלב זה נראה כי השקיעה מגיעה ל 0.98 ס"מ.

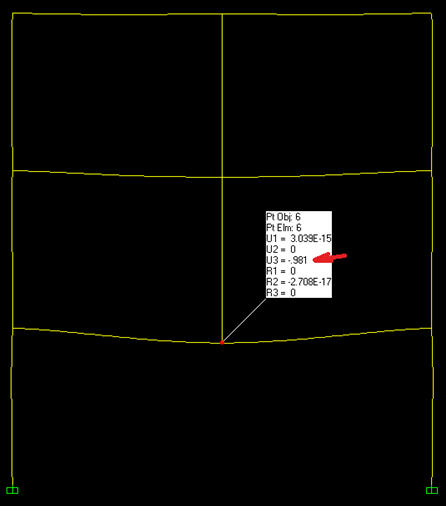
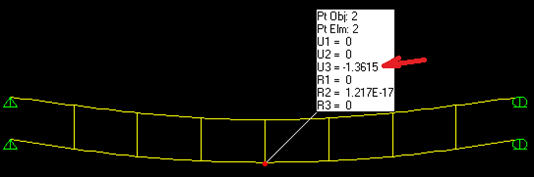
בשלב השישי והאחרון נעמיס את המבנה הגמור בעומסים הקבועים שאינן משקלן העצמי של התקרות וכן את העומס השימושי. השקיעה הכוללת של מרכז הקורה לאחר העמסת כל העומסים תהיה 1.39 ס"מ לעומת 1.07 ס"מ בחישוב סטטי של המצב הסופי ללא שלבים. כלומר השקיעה ה"אמיתית" גדולה ב 30% מהשקיעה המחושבת ללא שלבים. המומנט המקסימלי בשלב האחרון, בחישוב בשלבים, הוא 47.4 טון מטר והוא גדול בכ 20% מהחישוב הסטטי של המבנה במצבו הסופי.

נחזור עתה לדוגמא מעשית של חיזוק קורת בטון בפרופיל פלדה במהלך עבודת שיפוץ. נתונה קורת בטון במידות 20/30 ס"מ על 3 סמכים. מידות המפתחים 3 מ`. הקורה נושאת עומס של 2 טון/מ"א. מבקשים להצמיד לקורה פרופיל פלדה רגילה UNP 300 ולבטל את עמוד התמיכה המרכזי כך שהקורה תגשר על מפתח של 6 מ`. בחישוב על צד הביטחון נמסור את כל העמסים לקורת הפלדה.

מומנט מקסימלי במרכז הקורה יהיה אם כן (לעומס הוספתי את המשקל העצמי של הקורות): M = 2.2 * 36 / 8 = 9.9 t`m

מודול החתך של פרופיל הפלדה הינו כ 535 ס"מ^3 ומכאן נקבל את המאמצים בפלדה = 9.9 * 100000 / 535 = 1850 kg/cm2

בחישוב השקיעה נקבל כ 2.2 ס"מ. ואלה כמובן מאמצים גבוהים מהמאמץ המותר ושקיעה הגדולה מ L/350 מה שמחייב להגדיל את החתך.

כעת נבחן את שיטת החישוב בשלבים. בשלב הראשון נעמיס את קורת הבטון על 3 סמכים בעומס של 2 טון למ"א. את מהלך המומנטים של שלב זה נראה בתרשים הבא:

המומנט המקסימלי בשדה הוא כ 1.37 והמומנט השלילי מעל הסמך הוא כ-2.38 טון מטר. בשלב הבא נוסיף לקורת הבטון את פרופיל הפלדה. על מנת להקל על מראה המודל, נחבר את קורת הפלדה מעל קורת הבטון במספר חיבורים קשיחים, דו-פרקיים, שיבטיחו השוואת השקיעות בשלב הבא. מיקום המוטות בהתאם למיקום הברגים שיצמידו את הקורות. החיבורים האלה יציגו את הכוחות ההדדיים בין הקורות ויאפשרו לאחר מכן לבדוק את כוחות הגזירה הפועלים על הברגים המצמידים את קורת הפלדה לקורת הבטון.

בתרשים מתואר קו השקיעות ההתחלתי של מצב זה:

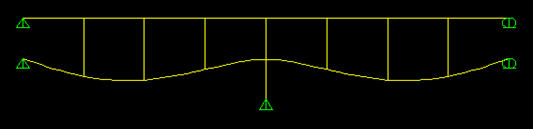
בשלב האחרון נסיר את עמוד התמיכה האמצעי ונקבל את חלוקת הכוחות בין שתי הקורות. בתרשים הבא נוכל לראות את מהלך המומנטים בשלב הסופי של החישוב הסטטי הלא ליניארי.

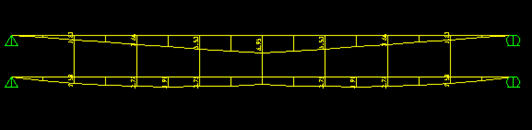
המומנט המקסימלי בקורת הפלדה הוא רק 6.95 t`m והמאמצים בפלדה יהיו בהתאם: M = 6.95 * 100000 / 535 = 1300 kg/cm2

המומנט המכסימלי בשדה של קורת הבטון יהיה כ 3.9 טון מטר, כאשר המומנט במרכז שהיה שלילי יהפוך לחיובי ושיעורו 2.95 טון מטר. כמובן שעל הקונסטרוקטור לוודא כי קורת הבטון עם ברזל הזיון הקיים, מסוגלת לשאת במומנטים החדשים. בחישוב זה מתקבל (כפי שמוצג בתרשים הבא) כי השקיעה המשותפת הסופית של שתי הקורות היא 1.36 ס"מ במרכז. מה שעומד בקריטריון השקיעה המותרת.

למרות ששתי הבעיות שהוצגו במאמר נראות שונות הרי מבחינה חישובית, בשיטת הבניה בשלבים, הן דומות. ההבדל היחיד הוא, שבשלב השלישי של הבעיה האחרונה, במקום הוספת אלמנטי מבנה, מבצעים הסרה של אלמנט (העמוד התומך).

לסיכום, קיימים מצבים בהם חישוב מבנה במצבו הסופי, אינו מייצג באופן נכון את האופן האמיתי של הביצוע בשלבים של המבנה. ההבדל בין שיטות החישוב הסטטי של מבנה במצבו הסופי לבין החישוב הסטטי הלא ליניארי של הבניה בשלבים, יכול להגיע לעיתים לעשרות אחוזים.

אשמח לקבל תגובות והערות לאמור לעיל וכן אשתדל לענות על שאלות שישאלו בפורום.