קורת וירנדל - שימושים וחישובים
תודה רבה לאינג' יעקב גרושקו על ההסברים.
הקדמה
כאשר קורת בטון מקבלת כוח גזירה מעבר ליכולת הבטון עצמו (Vrd1 או Vrd,c בתקן החדש) התפיסה של הבטון כחתך סדוק כבר לא מאפשרת מושגים כמו זרם גזירה ומאמצי גזירה (τ) אלא מחשבים את הקורה כאגד בו קיימים אלמנטים בעלי כוחות ציריים בלבד (גם בחישוב דחייה בו כן מתייחסים לנוסחא τ=(V×Q)/(I×b) החישוב ידבר על האלמנט המאחד בלבד – מוטות הפלדה, ולא על הבטון). כל ההבנה של מרחק d מפני הסמך, הקטנה βv, וכו' בגזירה ובחדירה נובעה מההבנה של מודל המסבך.
המינימליזם המאפיין את האגד הפלדה המוכר מתקבל הודות לכוחות הציריים העוברים באלמנטים ובכך מקטינים את החתך, גם בקורת בטון ניתן להגדיר סיב מתוח, סיב לחוץ ואלכסונים המתפקדים במתיחה ובלחיצה.
כאשר לא ניתן להפגיש אלמנטים בצמתים בהם ימסרו כוחות ציריים מאד לשני יש צורך בעברת כוחות אלו באלמנטי כפיפה.
בדומה לכך, חיבור אלמנטי אגד כך שצירי האלמנט לא נפגשים בנקדה אחת מכניס את האלמנט לכפיפה שבדרך כלל לא תאפשר יציבות.
כאשר נאלצים לבצע מערכת כזו האגד הופך חלקית למסגרת ונאלץ להתמודד עם כוחות מסוג אחר.
שימושים
השימוש הקלאסי הוא כאשר אנו מנסים לגשר מעל מפתחים גדולים אך עדיין ליצור קיר עם פתחים אדריכליים.
לדוגמא, כאשר עוברים ממודול של חניה עם מפתחים גדולים למודול של דירה עם עמודים צפופים יותר אך לא רוצים להעמיס את תקרת החניון בעמודים צומחים וגם תקרת טרנספורמציה עבה לא באה בחשבון, משתמשים בקירות הקומה בתור קורות אך כדי לאפשר פתחים למעבר יוצרים וירנדל. לפעמים מבנה פלדה ולפעמים מבטון.
בפלדה יש צורך בהגנה בפני אש ובעיגון הפלדה למערכות הבטון.

בתמונה: קורת וירנדל (צבועה צהוב) מעל הבריכה בבנין "שלווה" בחדש בירושלים בביצוע של י.ב.יובל.
במקרה זה השיקול היה אדריכלי אך גם פירוס הכוח (גזירה טהורה) איפשר את הצורה הזו.
שימוש מצוי הרבה יותר הוא העברת תשתיות, בעיקר תעלות מיזוג, דרך קורות במבנה.
אם הדבר מבוצע בתיאום זה מצוין.


בתמונה: הביצוע היה ללא תיאום תסבולת הקורה בגזירה נמוכה מהנדרש.
שיטת חישוב ע"י מודל
ניתן לבנות מודל בתוכנת אלמנטים סופיים שידמה את המוטות הציריים ואת אלמנטי הכפיפה בוירנדל.
לדוגמא: תקרה במפתח של 10 מטרים.

רוחב ההשפעה של הקורה: 10 מטרים.
התקרה בעובי 20 ס"מ ועומס נוסף של 200 ק"ג\מ"ר.
עומס שימושי: 300 ק"ג\מ"ר.
עומס שירות: 1 טון\מ"ר
עומס הרס: 1.46 טון\מ"ר.
הקורה עצמה במידות 30/100 ומשקלה 0.75 טון\מטר.
סה"כ עובר לקורה 15.65 טון\מטר.
(נתעלם מחישובי סדקים ושקיעות)
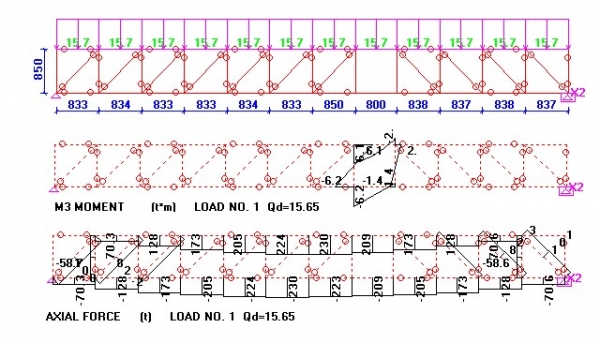
כל מוט שלא נוכל לתת פרק בשני צידיו משיקולי יציבות יעיד עליו שהוא אלמנט כפיפה ואז חשוב להתייחס לציר האלמנט ולא למידות הפתחים בלבד.
באמצעות מספר איטרציות בשיטת ניסוי וטעייה נגלה מה הסידור הנכון של הקורות, מה גובה הקורה מתחת התקרה ומה עובי הקורה מעל הפתח, נבין את כיוון סיבוב המומנטים בכל אלמנט ואיזה מומנט במשקוף מתקשר לאיזה מומנט באלמנטי הצד, מהם אורכי העיגון הדרושים וכו'.
נוכל לראות שהזיון הראש של הקורה\קיר כולו מתווספים על הזיון של הכפיפה ואפילו נוצרות התנגשויות. לצורך כך מומלץ לשרטט חתכים על דף חשבון בקנה מידה ולבחון הצטלבויות אלו.
חישוב ידני
להשאיר את הכל בידי הטכנולוגיה זה לא בריא. ניתן לחשב את הגזירה לפני הפתח בצורה הפשוטה של קורה על שני סמכים או יותר וע"י דמיון משולשים להבין מה כוח הגזירה לפני הפתח. כמובן שגם כאן חייבים להתייחס לציר האלמנט ולא הפתח עצמו.
גודל כל חגורה יקבע על פי החלטה במגבלת הגיאומטריה הקיימת וגובהן של החגורות לא חייב להיות אחיד כלל. במקרה זה בחרתי כי כולן תהיינה 30 ס"מ לנוחות החישוב.
כוח הגזירה נחלק בין החגורה העליונה לתחתונה לפי גודלם האמיתי אך מכיוון שהחישוב מתבצע להרס ניתן להחליט כמה כוח יעבור דרך כל חגורה.
באמצעות המרחק בין ציר לציר נדע כמה מומנט צריך להיות בכל אלמנט כאשר הוא מתחלק בין שני צידיו עם סימן מתחלף של פלוס ומינוס.
מומנטים אלו עוברים דרך צידי הפתח עד שנוצר מהלך רציף סביב הפתח.
כל קורה מחושבת בנפרד לגזירה, מומנט וכוח צירי.
כאן חשוב לשים לב תסבולת מקסימלית בגזירה (Vrd2 או Vrdmax) למשוואות הקלסיות של הכפיפה שלא עובדות לחגורה עליונה ותחתונה בהם יש לחץ\מתיחה בנוסף לכפיפה.
בצורה הפשוטה ניתן לחשב כך:
העומס בין נקודה A לנקודה B יגיע לסמך בנקודה A.
העומס בין נקודות B ו-C יאסף לציר C ויעבור לציר D.
העומס בין נקודות C ו-D יאסף גם הוא לנקודה D.
כל העומס ייצור מומנט על ציר D אך החגורות, העליונה והתחתונה יקבלו אותו במומנט.
לכן הנוסחה תהיה:
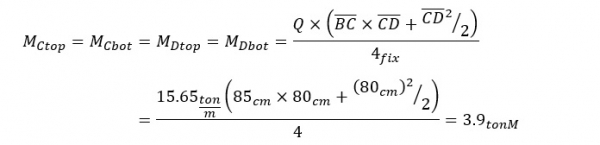
זהו ממוצע של המומנטים שהתקבל בתוכנה.
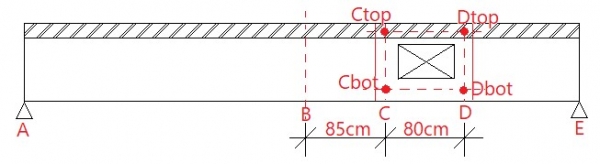
ניתן גם לראות את הדברים אחרת אך התוצאה זהה:
המומנט לפי סכימה פרקית, במרכז המפתח ייתקבל מומנט של 195.6 טון*מטר (Md).
יועץ המיזוג הכניס פתח בגובה של 40 ס"מ ברוחב 50 ס"מ במרחק של 3 מטר מהסמך.
חישוב הגזירה בקצה יהיה 78.25 טון (Vd). בדמיון משולשים אפשר לקבל בשני קצוות הפתח את כוח הגזירה.
מכיוון שהחגורה מתחת ומעל הפתח הם בגובה 30 ס"מ, גם את הצדדים ניקח בצורה זהה ואז החישוב יתייחס לפתח של 80 ס"מ (15 ס"מ לציר החגורה).
כוח הגזירה בצד ימין הוא 25.8 טון ו-13.3 טון בצד שמאל של הפתח.
בצורה דומה, מומנט מימין לפתח 174.3 טון*מטר ומשמאל 190 טון*מטר.
לבדיקה ניתן לבדוק שיקול כוחות אנכיים:
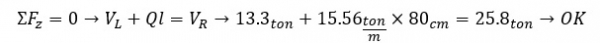
ובצורה דומה את המומנטים:
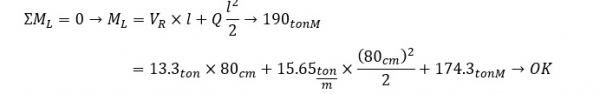
ועכשיו ניתן לראות את צמד הכוחות בכל צד לפי זרוע של 85 ס"מ (לפי בערך w=0.2)

כוחות בצד שמאל: C,L = T,L = M,L\Z = 223.5 ton
בצד השני באותו אופן נקבל 205 טון.
הכוחות בינהם יהיו: delta,C = delta,T = C,L - C,R = 18.4 ton.
המומט שיהיה בפינות: Mi = delta,T * 85cm\4fix = 3.9 ton*m.
כדי לדעת מה מיקום המומנט (פנימי או חיצוני) צריך אינטואיציה של הקו האלסטי:

חישוב החגורות
חישוב חגורה במידות 30*30 נותנת תסבולת מקסימלית לגזירה, כל חגורה 36 טון.
אם הפתח היה במרחק של 145 ס"מ מהסמך (מרחק ציר מהסמך 130 ס"מ) כוח הגזירה בשתי החגורות היה גדול מהתסבולת המקסימלית Vmax ולכן למיקום הפתח שיקול מכריע בהצלחת האלמנט.
עכשיו נותר לחשב בכל חגורה את כוחות הגזירה והמומנט לפי המידות שלה וכמובן גם את הזיון האורכי של הסיב התחתון.
לא נכנס לכל החישוב, אך לדוגמא את צד שמאל של הפתח נחשב לפי כוח גזירה של delta,C = delta,T = 18.4 ton ומומנט של Mi = 3.9 ton*m.

נידרש חישוק של 23.2 סמ"ר\מטר (בערך ɸ14@12.5cm) שוזה לא מעט בכלל, מוטות 3ɸ16 וכמובן לא לשכוח את החישוקים הרגילים של הקורה ɸ12@25.
כאשר הזיון ראשי של הקורה (קורת קמץ) הוא בערך 66 סמ"ר (3x5ɸ25) השילוב בין המוטות האורכיים למוטות הוירנדל כלל לא פשוטות. קיימות הצטלבויות רבות ויש לוודא כי כל ההצטלבויות אפשריות.
חגורה תחתונה שמכילה מתיחה בנוסף למומנטים צריכה להיות מחושבת לכך.
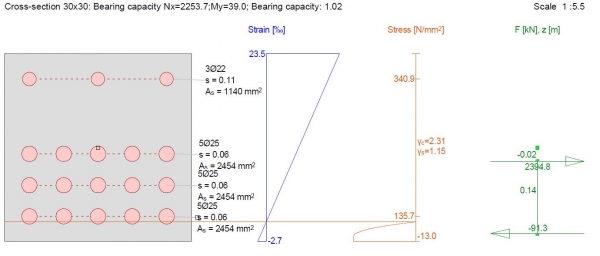
חגורה עליונה לוקחת בחשבון גם את התקרה.
החישוב בוצע ללא התייחסות לקשיחות הקורות היות והפתח ניתן במרכז הקורה אך במידה ונרצה לשחק עם ערכי המומנט כדי להקל על החגורה התחתונה שגם כך מלאה במוטות האורכיים נוכל לשנות את מיימדי החגורות ואיתם גם את הכוחות שיעברו דרכם.
סיכום
השימוש במסבך וירנדל דורשת חישוב מפורט ומדויק.
פרטי הזיון המורכבים שחוצים אחד את השני מחייבים שרטוטים בקנה-מידה כדי לבדוק את היתכנות הפתרון ולפעמים ביצועית לא ניתנים ליישום.
בחירת מיקום הפתח קריטית לעמידת הקורה בכוחות התכן.
למאמרים מקוצעיים נוספים של אסף דסברג:



















