האם בניין שתוכנן לפי התקן - יעמוד ברעידת אדמה בדרגה 7.0 ?

האם בניין שתוכנן לפי התקן יעמוד ברעידת אדמה בדרגה 7.0 ?...
האם המבנה הזה יעמוד ברעידת האדמה שהיתה לאחרונה בהאיטי ?...

לעיתים מזומנות (במיוחד לאחר רעידת אדמה חזקה וכאלה היו רבות בשנים האחרונות), אני נשאל שאלות כאלה או דומות, על ידי לקוחות, ידידים ואפילו קולגות. תשובותיי המתחמקות והלא חד משמעיות גורמות לצד השואל להרים גבה בתמיהה. הרמת גבה זו גורמת לי לתחושה, שזה שנמצא מולי, חושב שאני לא מבין שום דבר בתחום. חשבתי, שאולי כדאי לכתוב על כך מאמר קצר על מנת שאוכל להפנות אליו את השואל.

רעידות אדמה נוצרות עקב תזוזות ב"לוחות" המהווים את קליפת כדור הארץ. התזוזות מייצרות מאמצים שעלולים להשתחרר כאשר הלוחות נשברים ,מתנגשים וכד`. האנרגיה שמשתחררת, גורמת להתפשטות של גלים בקרקע שעוצמתם הולכת ודועכת עם המרחק ממרכז הארוע.

חוקרים רבים עסקו בדרוג עצמת הרעידות וקיימים מספר סולמות לדרוג, כאשר הסולם המוכר ביותר הוא סולם ריכטר. סולם נוסף שמקובל יותר בשימוש כיום הוא סולם "מומנט - מגניטודה". העוצמה שמתבטאת בסולם היא תוצאה של נוסחא לוגריתמית שהפרמטרים שלה הם: המרחק מהמרכז, עומק הארוע , תזוזת הקרקע במרחק של 100 ק"מ מהמרכז וזמן המחזור של הרעידה במרחק זה. הדרגה של רעש האדמה מבטאת למעשה את כמות האנרגיה שהשתחררה, אבל לא בהכרח את התאוצות של הקרקע באתר מסוים. תגובת מבנה לרעידת הקרקע, עליה הוא מבוסס, תשתנה בהתאם לנתוני הרעידה שניתן להציגה באקסלרוגרמה שהיא רישום הסטורית תאוצת הקרקע.

גם אם נבחון שתי אקסלרוגרמות שנרשמו במרחק זהה ממרכז הרעש ,(נניח אחת מצפון ואחת מצד דרום), לא בהכרח נקבל זהות ברישום כי גם לסוג הקרקע, לשכבתיות ולגיאולוגיה המקומית יש השפעה על אופי הרעידה. לכן, ניתן לומר, שגם שני מבנים זהים לחלוטין ואשר נמצאים במרחק זהה ממרכז הרעש לא בהכרח יגיבו בצורה זהה.

הנתונים שישפיעו על התנהגות המבנה הם משך הרעידה הכולל, תאוצות מקסימליות, זמן מחזור ממוצע של הרעידה והצורה הכללית של האקסלרוגרמה. גם נתוני המבנה עצמו ישפיעו על התנהגותו ברעידה כלומר: גובהו, מסתו, העומסים האחרים הפועלים עליו בזמן הרעידה, חוזק האלמנטים התומכים אותו וכיו"ב.

מתוך אקסלרוגרמה של רעידה מסוימת, בנקודה מסוימת, ניתן לחשב באופן נומרי את הסטורית הדפורמציות של מערכת בדרגת חופש אחת (מערכת מסה - קפיץ עם או בלי מרסן). אם נרשום את ההזזה המקסימלית של התגובה ונבצע פעולה זאת למספר גדול של מערכות כאלה אבל עם זמן מחזור שונה (שנויים של המסה או קשיחות הקפיץ) נוכל לייצר עקום שמתאר את התזוזה המקסימלית כפונקציה של זמן המחזור וזאת עבור האקסלרוגרמה המסוימת. עקום זה נקרא "ספקטרום התגובה". מתוך עקום זה ניתן לייצר עקומות של פסאודו-מהירות ושל פסאודו - תאוצה מקסימלית, כפונקציה של זמן מחזור. עקומות אלה אינם של מהירות ותאוצה מקסימליות של מערכת מסה - קפיץ, אלא הערכים של עקומות אלה מבטאים את האנרגיה הקינטית ואת הכח השקיל, בהתאמה, שיש להפעיל על המסה לקבלת התזוזה המקסימלית.

אם באזור מסוים יש מספיק רעידות אדמה, ניתן לייצר מהאקסלרוגרמות המתקבלות את העקומות שהוזכרו לעיל וניתן לייצר עקומה סטטיסטית שתיתן ערכם ממוצעים וסטיות תקן, דבר שיאפשר לייצר תקן מקומי שיגדיר את הערכים וכן את הכח הסטטי השקיל שיש להפעיל על מבנה ,עם זמן מחזור נתון, על מנת לקבל את הדפורמציה המקסימלית. בדיקת עמידות מבנה לרעידה שיכולה לקרות במקום אחר בעולם, לא בהכרח תהיה רלוונטית באשר הסכוי שרעידה כזאת תקרה בישראל יכול להיות אפסי.

יחד עם זאת, על מנת להמחיש את הבעיתיות שיש במתן מענה לשאלה שבכותרת המאמר ,נבחן דוגמא כדלקמן: נבחר במבנה מסגרת מרחבית מבטון מזוין, של 4 קומות. הבנין בן 5 מפתחים של 6 מ` בכוון הראשי ו 4 מפתחים של 5 מ` בכוון המשני. עומסי תקרות ,מעבר למשקל עצמי, עומס קבוע בשיעור של 250 ק"ג/מ"ר ועומס שימושי 500 ק"ג/מ"ר.

בשלב הראשון נחשב את המבנה בחישוב סטטי ,על פי התקנים ,לעמסים רגילים (קבוע, שימושי ,רעידות אדמה ,רוח וכד`). במסגרת הקומבינציות של מצבי העמיסה, מוסיפים את עמסי התכן האופקיים הפועלים במרכז המסה של התקרות כפי שנדרש בתקן ישראל 413. בתרשים הבא אנו רואים את המבנה על אלמנטיו השונים לקראת החישוב הסטטי:

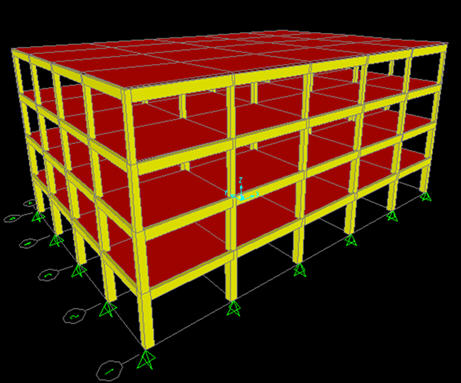
בהפעלת הכח הסטטי השקיל התייחסתי לזמן התנודה הבסיסי של המבנה כפי שנתקבל מהאנליזה של צורות התנודה - 1.083 שניות. פרמטרים נוספים שבחרתי בהצגת הדוגמא:

מקדם תאוצת קרקע אופקית חזוייה: Z=0.15
מקדם השתית באתר: S=1.5
מקדם חשיבות המבנה: I=1.0
מקדם הקטנת הכוח: 5.5=K (רמת משיכות בינונית למסגרת מרחבית כפיפה מבטון מזויין)

מקדם השכיחות לעומס שימושי: Kq=0.5

נבחן את התזוזות האופקיות המתקבלות בחישוב הסטטי בדופן הימנית של המסגרת האמצעית בכוון – X

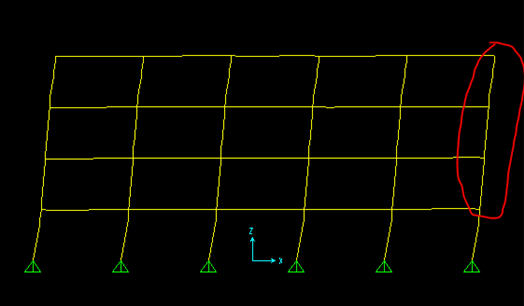
התזוזות הן כדלקמן:

קומה ראשונה: 0.94 ס"מ

קומה שניה: 1.4 ס"מ

קומה שלישית: 1.9 ס"מ

קומה רביעית: 2.56 ס"מ

ההסטה הקומתית המקסימלית תהיה אם כן 0.66 ס"מ בקומה העליונה.

ההסטה המקסימלית המותרת הינה על פי התקן 1/250 מגובה הקומה כלומר: 350/250 = 1.4 ס"מ.

גם בדיקת האלמנטים לעמידה בכוחות והמומנטים מראה כי המבנה עומד בדרישות התקנים.

בשנת 1994 התרחשה בנורת`רידג` שבקליפורניה רעידת אדמה חזקה - 6.7 בסולם "מגניטודה". ברעידת אדמה זאת נרשמו תאוצות קרקע מהגבוהות שהיו אי פעם בצפון אמריקה . התאוצות הגיעו עד כדי 1.7g. להלן רישום של תאוצת הקרקע בנקודה מסוימת באזור:

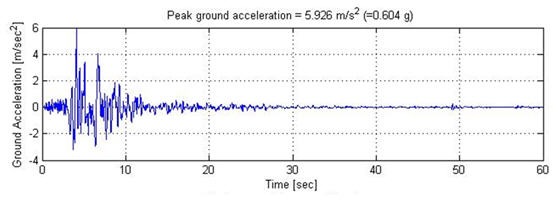
כאן התאוצה המקסימלית היא כמעט 6 מ` לשניה².

ננסה לבחון האם המבנה שבדוגמא יכול היה לעמוד ברעידה זאת. לצורך זה נריץ את המבנה בהרצה דינמית לקבלת "הסטורית התגובה". הריצה מבוצעת למשך 60 שניות בצעדים של 0.01 שניה. בתרשים הבא נראה את תגובתה של הנקודה הימנית העליונה במסגרת המרכזית בכוון X:

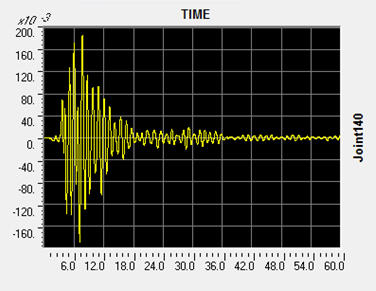
ההזזה המקסימלית שמתקבלת היא כ 18.9 ס"מ לאחר כ 7 שניות. אם נבחן את שתי נקודות הקצה של הקומה העליונה, ונרווח את ציר הזמן נקבל את התרשים הבא:

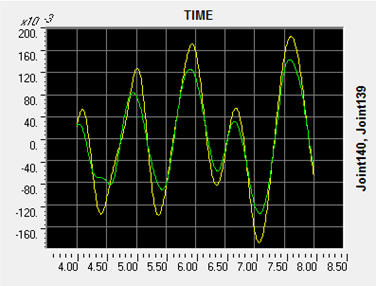
מתוך תרשים זה נוכל לראות שההסטה הקומתית תהיה 5.3 ס"מ. (ההפרש המקסימלי בין הגרפים) וברור שהסטה קומתית זאת גבוהה פי כמה מההסטה המותרת בתקן (1.4 ס"מ למקרה זה).

גם בדיקת אלמנטי המבנה לעמידות במומנטים ובכוחות הגזירה המקסימליים המתקבלים ,תראה בברור שתסבולתם נמוכה מהעומסים שפועלים עליהם.

הבעיה בתוצאות המתקבלות, נעוצה בכך שהחישובים הם אלסטיים ליניארים. כלומר המבנה יכול לקבל כוחות והזזות ללא קשר לכוחות המקסימליים שהחתכים מסוגלים לקבל. מתוך כך ברור, כי המבנה שיגיב לרעידה הנ"ל, יפסיק להתנהג באופן אלסטי ומהר מאד יכנס לתחום הפלסטי.

עתה, אחרי שחישבתי את המבנה גם סטטית וגם דינמית ,האם אני יכול לענות על השאלה המתבקשת: "האם המבנה יעמוד ברעידת האדמה כפי שהיתה בנורת`רידג`" ? בוודאי שלא. אני יכול לומר שהמבנה יינזק ויסדק אבל עד שלא אבצע חישוב אלסטי - פלסטי לא ליניארי, לא אוכל לומר האם המבנה יעמוד על תילו או יקרוס על יושביו.

החישוב האלסטי - פלסטי והלא ליניארי, בהחלט אפשרי, אבל מצריך השקעה גדולה יותר הן בהערכת התכונות של הפרקים הפלסטיים והן במשאבי מחשב (ואולי אבצע חישוב שכזה למאמר המשך בעתיד).

לסיכום

האם אפשר לענות על השאלה שבכותרת המאמר ? להערכתי, גם אם מבצעים חישוב אלסטי דינמי לרעידה ספציפית, לא תמיד ניתן לענות באופן נחרץ על השאלה. מה שניתן לומר זה את התשובה המתחמקת ,אבל הברורה והנכונה בהחלט, ש"מבנה שתוכנן לעמידות ברעידות אדמה על פי התקן, יעמוד ברעידה בצורה טובה יותר מאשר אם לא היה מתוכנן. גם פרטי בנין שיסופקו כנדרש בתקן יאפשרו למבנה לקבל עיוותים פלסטיים גדולים יותר, מה שיבטיח סכויי שרידות גבוהים בהרבה ממבנה החסר את הפרטים האלה".

אשמח לקבל תגובות והערות לאמור לעיל וכן אשתדל לענות על שאלות שישאלו בפורום CivilEng.