הצטרפו ל WhatsApp של קהילת ענף הבנייה והתשתיות בישראל. כאן >>

תכנון מבנים כנגד התמוטטות בשרשרת

התמוטטות בשרשרת הינה אירוע נדיר המחייב, מצד אחד עומס פתאומי גדול הגורם לנזק נקודתי ומצד שני מבנה החסר בהמשכיות, משיכות ויתירות בחוזקם של האלמנטים השונים שבו, היכולים להתנגד להתפשטות הנזק. אבל, כשמקרה כזה קורה, צפויים נפגעים רבים, כאשר המבנה כולו או חלקו הגדול יקרסו.

תחילת ההתעניינות ההנדסית בנושא החלה כבר לפני למעלה מ 40 שנה, בעקבות התמוטטות אגף בבנין מגורים רב קומות Ronan Point בלונדון אנגליה. אירוע זה החל כתוצאה מפיצוץ גאז ביתי שדלף וגרם להרס קיר נושא.הארוע התרחש החל בקומה ה -18 מתוך 22 הקומות וגרם להתמוטטות הקומות באגף שמעל אבל, הרגמות שנפלו כלפי מטה, גרמו להמשך של תגובת שרשרת לגבי הקומות שמתחת. אמנם רק 4 הרוגים היו באירוע זה, אבל התקן הבריטי הוסיף מסמך הקובע כי במידה והסרת אלמנט במבנה יכולה לגרום להתמוטטות בשרשרת שלו, הרי האלמנט הינו אלמנט תמיכה מרכזי ויש לתכננו לעמידות בפיצוץ.

את האגף שהתמוטט ניתן לראות בתמונה הבאה:

ההתענינות בנושא בארה"ב החלה ב 1995 עקב פיצוץ הטרור של משאית תופת בסמוך לבנין הממשל הפדרלי באוקלהומה סיטי, באירוע זה נהרגו 168 אנשים, שמרביתם לא נהרגו מההדף ,אלא מהתמוטטות בשרשרת של מרבית המבנה ,שהחל בהרס של עמוד החזית. תמונות של המבנה לפני ואחרי הפיצוץ ניתן לראות במאמר קודם שלי באתר זה מבני מגן. אירוע הטרור הגדול בתאריך 11/9/2001 בו קרסו מגדלי התאומים בניו יורק ונפגע מבנה הפנטגון בוושינגטון הבירה, מפגיעת מטוסי נוסעים, כאשר מספר ההרוגים היה בסביבות 3000, הגביר את העיסוק בנושא והחלו לצאת הנחיות לתכנון מבנים חדשים ולבדיקת מבנים קיימים.

תאור התמוטטות בשרשרת

האירוע מתחיל באלמנט מבנה שניזוק בצורה קשה ואינו יכול להוסיף ולשמש בתפקידו. המבנה מחפש דרך עקיפה לשאת את העמס על ידי העברת העומסים לקורות ולעמודים סמוכים. כאשר אלה אינם מסוגלים לשאת את תוספת העמס הפתאומית הם נהרסים והתופעה ממשיכה להתפתח עד לכדי הרס כולל של המבנה או של חלק גדול ממנו. במהלך העשור האחרון החלו מספר סוכנויות בארה"ב לפתח קוים מנחים להתמודד עם התופעה של התמוטטות בשרשרת..

American Society of Civil Engineers ASCE 7-05

General Services Administration GSA
Department of Defense - UFC 4-023-03

מדריכי התכנון השונים, דורשים עמידות כנגד התופעה אבל לאו דוקא עמידות הרכיבים כנגד אירוע נקודתי, אלא, בהנחה שהאירוע התרחש, יש צורך לבדוק ולוודא שהתמוטטות בשרשרת לא תיגרם. לדוגמא, נדרש המתכנן להוכיח כי היעלמות פתאומית של עמוד חזית במבנה, תגרום אולי לדפורמציות גדולות אבל לא להתמוטטות של כל המבנה. הדרישות מתייחסות לא רק למבנים חדשים אלא נדרש גם לבדוק ולחזק בהתאם מבנים קיימים. קיימות שתי גישות מרכזיות להתמודד עם בעיית ההתמוטטות בשרשרת:

הגישה הישירה

כאשר יש מידע מודיעיני או סקר סיכונים לגבי האיום המוצב בפני המבנה, ניתן לחשב ולתכנן את האלמנטים התומכים את המבנה, כך שיהיו עמידים כנגד התרחשות האירוע. כמו לדוגמא, חישוב ותכנון הקירות הנושאים כנגד פיצוץ מכונית תופת וכד`.

הגישה הבלתי ישירה

כאשר אין מידע לגבי איום ספציפי, אזי ניתן לחזק את המבנה במספר שיטות שיתוארו להלן או בשילוב ביניהן. הנטיה כיום היא לבחור בגישה הבלתי ישירה ,כך שהמתכנן אינו צריך להתמודד עם האיומים וחישוב השפעתם על אלמנטי המבנה.

שיטות תכן כנגד התמוטטות בשרשרת

הוגדרו שלש גישות עיקריות לתכן וחישוב כנגד התופעה:

כוחות קשירה - Tie Forces TF

נתיב חילופי - Alternate Path AP

חיזוק מקומי - Enhanced Local Resistance ELR

TF - כוחות הקשירה משמשים להגברת ההמשכיות, המשיכות והיתירות של אלמטי המבנה. זאת, על ידי דרישה לקבלת כוחות מתיחה שיאפשרו קשירה של אלמנטים במבנה, ויאפשרו העברת העומסים מהאזור שניזוק לאלמנטים שלא ניזוקו. כך למשל תקרות שנשענות על קורות , בהיעדר קורה נושאת, תוכלנה לשאת את העמסים על ידי פיתוח כוחות מתיחה תוך שקיעות גדולות. (עקום שרשרת - catenary action) כוחות קשירה אלה יכולים להתקבל גם על ידי ברזל זיון הקיים ממילא בתקרות הבטון, אך יש לוודא כי הזיון הינו המשכי ומעוגן בקצוות לאלמנטים אחרים.

AP - בשיטה זאת משתמשים לחישוב אלמנטי מבנה כנגד הסרה פתאומית של עמוד או קיר נושא. זאת, על ידי העברת הכוחות לעמודים סמוכים תוך גישור מעבר לאלמנט שהוסר.

המדריך נותן אינדיקציות לגבי איזה מהעמודים יש להסיר, לצורך החישוב, בתלות בסוג המבנה ובאופי התפוסה שלו (הרחבה בהמשך).

ELR - הגדלת תסבולת עמודים וקירות נושאים הן לגזירה והן לכפף במטרה לצמצם את הסיכון והסבירות לנזק הראשוני היוזם את תחילת ההתמוטטות.

שיטת החישוב והתכן, או שילוב בין השיטות, מותנה בסוג המבנה ובאופי התפוסה שלו. ככל שהמבנה מכיל פחות אנשים ואינו חיוני בזמן חירום, כך תקטן הדרישה וככל שהמבנה חיוני יותר וצפוף יותר כך יוחמרו הדרישות, ויהיה צורך לשלב בין כמה שיטות .

עומסי תכן לחישוב כנגד התמוטטות בשרשרת

בחישובים אלה נדרשים המתכננים להכפיל את העומסים במקדמי ביטחון חלקיים כדלקמן:

W=1.2 * D + 0.5 * L

כאשר:

W = עומס התכן

D = עומס קבוע

L = עומס שימושי

אפשרויות חישוב בשיטת הנתיב החילופי - Alternate Path AP

סטטית ליניארית Linear Static LS

חישוב סטטי רגיל הכולל הכפלת העומס ב"מקדם הגברת העומס" (LIF )

החישוב מתבצע על מודל שחסר את האלמנט שהוסר (עמוד,קיר נושא)

סטטית לא-ליניארית Nonlinear Static NLS
לאחר בניית מודל (ללא האלמנט שהוסר) הכולל את התכונות הלא-ליניאריות של החמר והגיאומטריה, מכפילים את העומס במקדם הגברה דינמי (DIF) האמור לכלול את השפעת כוחות האינרציה. לאחר קבלת תוצאות החישוב בודקים האם האלמנטים מסוגלים לעמוד בדפורמציות ובכוחות הפנימיים

דינמית לא-ליניארית Nonlinear Dynamic NLD
חישוב דינמי הכולל שני שלבים:
א. העמסה איטית של המבנה תוך החלפת העמוד בכוח ומומנטים חלופיים, עד להגעה לשוי משקל.
ב. הסרת הכוח והמומנטים באופן מהיר תוך השארת עומסי התכן. החישוב הדינמי נמשך עד לקבלת מצב מנוחה לאחר מכן בדיקת הדפורמציות וזויות הסיבוב בפרקים הפלסטים לבחינת העמידות בקריטריונים.

באנליזה זאת נדרש המתכנן להניח את תכונות הפרקים הפלסטיים, אם כי קיימת אפשרות שהתוכנה תבצע בחירה אוטומטית של תכונות אלה. יש לספק פירטי זיון שיאפשרו התפתחות של פרקים פלסטיים כפי שאנו מעונינים, כמו למשל,מתן חישוקים צפופים יותר באזור הפרק על מנת לאפשר לפרק סיבוב פלסטי טרם הרס בגזירה.

דוגמא

דוגמא לחישוב של השפעת הסרת עמוד בשיטה דינמית לא-ליניארית Nonlinear Dynamic NLD

להמחשה, נבחר במבנה מסגרת מרחבית מבטון מזוין, של 4 קומות. הבנין בן 5 מפתחים של 6 מ` בכוון הראשי ו 4 מפתחים של 5 מ` בכוון המשני. עומסי תקרות, מעבר למשקל עצמי, עומס קבוע בשיעור של 250 ק"ג/מ"ר ועומס שימושי 500 ק"ג/מ"ר. למסגרות החזית נוסף עומס קבוע של קירות מסך.

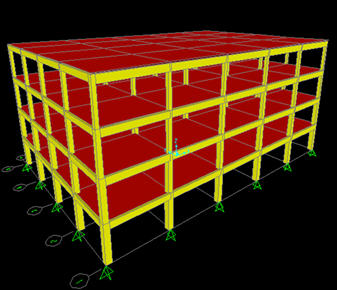
בשלב הראשון מתכננים את המבנה בחישוב סטטי ,על פי התקנים ,לעמסים רגילים (קבוע, שימוש, רעידות אדמה, רוח וכד`). במסגרת הקומבינציות של מצבי העמיסה, מוסיפים את עמס התכן כנגד התמוטטות בשרשרת. מתוך תוצאות החישוב שולפים את הריאקציות (כח צירי, מומנטים) שמפעיל האלמנט המתוכנן להסרה, על הבנין. בתרשים הבא אנו רואים את המבנה על אלמנטיו השונים לקראת החישוב הסטטי. כמובן שבהמשך לקבלת תוצאות החישוב הסטטי, קובעים את מידות האלמנטים ואת ברזל הזיון.

בשלב הבא מסירים את האלמנט ומפעילים על המבנה את הריאקציות ששלפנו מתוצאות החישוב לעיל, כעומסים חיצוניים. בחישוב הדינמי, העמיסה נעשית הדרגתית באופן ליניארי בפרקי זמן ארוכים ביחס לאופני התנודה של המבנה. זאת על מנת לדמות העמסה סטטית רגילה.

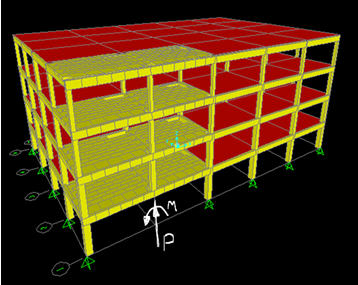
לצורך החישוב הדינמי יש לעשות מספר שנויים במודל המבנה.

מאחר ובתוכנות האלמנטים הסופיים, המסה של האלמנט מתרכזת בשתי קצותיו, יש לוודא כי האזור בו צפויות הדפורמציות ,כתוצאה מכוחות האינרציה, יחולק כך שהשפעת המסות תוכל לבוא לידי ביטוי. במקרה זה חולקו שני המפתחים השמאליים בחזית, לחלקים באורך של 1 מטר. יש למקם פרקים פלסטיים באותם המקומות הצפויים להינזק. יש כמובן אף להגדיר את תכונות הפרק הפלסטי. הגדרת הפרק הפלסטי מחייבת קביעה של עקום המומנט כנגד זוית סיבוב. ישנן תוכנות שכוללות אפשרות אוטומטית לבחירת פרק פלסטי על פי הטבלאות אשר במדריך FEMA-356.

יש לציין כי הגדרות אלה, מתאימות להתפתחות פרקים פלסטיים במהלך רעידת אדמה. כאשר מדובר בתנועות ציקליות של הפרק ובזויות סיבוב קטנות יחסית ואינן מתאימות למקרה זה. התנהגות הפרק הפלסטי כאן, מתאימה יותר לפרקים פלסטיים המתהוים במבני מגן כאשר מהירות היוצרות הפרק גדולה ביותר וזויות הסיבוב שמתפתחות יכולות להגיע לערכים גבוהים. בכל מקרה חשוב לציין כי הנחה נכונה של המיקום ותכונות הפרקים הפלסטיים הינה קריטית לקבלת תוצאות אמינות בחישוב זה. במודל זה גם הוחלפו פלטות התקרה, באזור הצפוי להינזק, ברשת קורות ברוחב 1 מ` כל קורה. כאשר המשקל המרחבי של הבטון בקורות אלה חולק לשניים. הסיבה לכך היא שבתוכנה זאת אין אפשרות להצבת פרקים פלסטיים באלמנטי לוחות אלא רק באלמנטי מוטות בלבד.

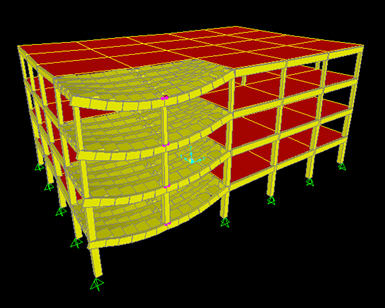
לאחר מכן מבצעים חישוב דינמי לא ליניארי של המבנה להסרת העמוד כך שהעומסים הפועלים עליו נשארים עומסי הגרוויטציה. החישובים הינם עוקבים, כאשר תנאי ההתחלה של הריצה השניה, הינם תנאי הסיום של המצב הראשון (מבחינת שקיעות , כוחות פנימיים וכד`). בתרשים הבא נראה את צורת השקיעה של האזור השמאלי של חזית המבנה, בגמר ההרצה הדינמית.

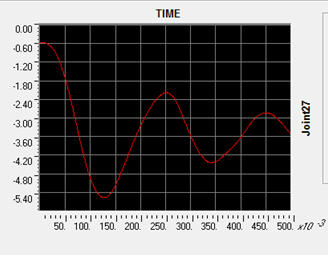
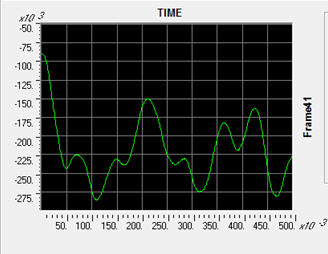
בגרף הבא נוכל לראות את תגובת הנקודה שמעל העמוד שהוסר מרגע ההסרה. הנקודה שקעה עד לשקיעה מקסימלית של כ 5.6 ס"מ בתוך פרק זמן של כ 120 מילישניות. לאחר מכן מתרסנת השקיעה לכדי כ 3.6 ס"מ שקיעה סופית.

ראוי לציין כי מדובר בשקיעות קטנות יחסית וחישוב הפרקים הפלסטיים מראה כי הסיבוב שלהם אינו גדול ולא מתקרב לסיבוב התסבולת המקסימלי שמעבר לו הקורה היתה מתמוטטת. הסיבות לתוצאות (טובות) אלה הם:
1. המסגרת המרחבית תוכננה גם כנגד רעידות אדמה.
2. תקרות הבטון שבדרך כלל נתמכות על ידי קורות החזית, נכנסות לעזרת הקורות על ידי פיתוח שקיעות ופרקים פלסטיים.

אם נניח שאת הכוחות האופקיים, עקב רעידת אדמה, היה מקבל גרעין הנמצא במרכז המבנה, היתה מסגרת החזית מתוכננת בעיקר לכוחות גרוויטציה מה שהיה גורר אחריו קורות צנועות יותר וחוסר בברזל זיון מספק, במיוחד מוטות תחתונים באזור מיקום העמודים, בנוסף, אם במקום התקרות המקשיות מבטון מזויין היינו משתמשים, למשל, בפלטות טרומיות, אזי סכויי המבנה לעמוד בפני התמוטטות בשרשרת היו קטנים באופן משמעותי.

בגרף הבא אנו רואים את הלחץ הפועל על העמוד הפנימי של המסגרת החיצונית. הלחץ גדל בתוך 110 מילישניות מ כ-90 טון עד ל-285 טון. יש כמובן לוודא כי העמודים הסמוכים לעמוד שהוסר, מסוגלים לשאת את תוספת העומס הזאת. אך יש לזכור שהעמוד תוכנן לעומסי תכן רגילים
( 1.4xD+1.6xL ) בעוד שחישוב זה נעשה עם עומסי תכן קטנים יותר ( 1.2xD+0.5xL ).

סיכום

בעשור האחרון גברה מאד ההתענינות ההנדסית לתכנון מבנים למניעת תופעת ההתמוטטות בשרשרת.

מדריכים שונים מציעים קווים מנחים לתכנון ,על מנת להתמודד עם התופעה, כאשר רמת הטיפול בשיטות חישוב שונות ובשילוב ביניהם, תלויים בסוג המבנה ובאופי התפוסה שלו. בישראל (למודת המלחמות ופיגועי טרור) ,טרם יצאו הנחיות הנדסיות אך יש לשער כי לא ירחק היום וגם מהנדסי המבנים שלנו יאלצו להתמודד עם נושא זה שהינו מאתגר במיוחד.

אשמח לקבל תגובות והערות לאמור לעיל וכן אשתדל לענות על שאלות שישאלו בפורום.