עמידות בהדף של אלמנטים לחוצים
באופן מסורתי תוכננו אלמנטי בטון מזוין כמו עמודים, קירות נושאים, ניצבי גשרים, לקבלת כוחות לחיצה ציריים גדולים מהמשקל הנישא מעליהם והעברתו למפלסים נמוכים יותר ועד היסודות.
עם השתפרות כלי החישוב החלו, ממחצית המאה הקודמת, להתיחס גם לכוחות אופקיים הנובעים מעומסי רוח ורעידות אדמה ולשלב בתכנון האלמנטים הלחוצים.
בשני העשורים האחרונים גברה ההתענינות בעומסי אימפקט והדף פיצוץ (בעיקר בעקבות התפתחות הטרור העולמי), זאת מאחר ואנו דנים באלמנטים החשובים ביותר ליציבותו של המבנה וקריסה, למשל, של אחד מהעמודים יכול להביא להתמוטטות כוללת של המבנה ולאובדן חיי אדם רבים.
כמו כן בשנים האחרונות גדלה הנטיה לתכנון מבנים רבי קומות עם קומת כניסה גבוהה במיוחד, דבר הגורם להגדלת הסיכון, מהדף פיצוץ, של העמודים והקירות הנושאים, הן מעומסי הלחיצה הגבוהים והן עקב המפתחים הגדולים של העמודים לעומסים אופקיים צידיים.
מטרת חישוב לעמידות בהדף של פלטות וקורות, היא להעריך את התגובה של האלמנט לעומס הניצב לצירו ולחשב את הדפורמציות והמשיכות (מנת הדפורמציה המקסימלית עם הדפורמציה האלסטית המקסימלית) ומתוך כך להעריך את דרגת הנזק והסיכון להרס כולל.
המדריך האמריקאי לתכנון מבני מגן מכיר בחשיבות עמידות עמודים כנגד הדף פיצוץ ומגביל את המשיכות המקסימלית המותרת ל- 3.
טבעי להניח כי בשילוב של עומס צידי בניצב לציר האלמנט יחד עם עומס לחיצה צירי, יגדיל עומס הלחיצה את הדפורמציות האופקיות וככל שתגדל הדפורמציה יגדל המומנט הנגרם על ידי כח הלחיצה (אפקט הנקרא פי-דלתא) ויתווסף למומנט הנגרם מהעומס האופקי.
יחד עם זאת הלחיצה הצירית, בחתכי בטון מזוין, דוקא מקשיחה את החתך ובתחום לחצים מסוים אף מגדילה את מומנט התסבולת, כפי שמוצג בדיאגרמת האינטרקציה להלן:
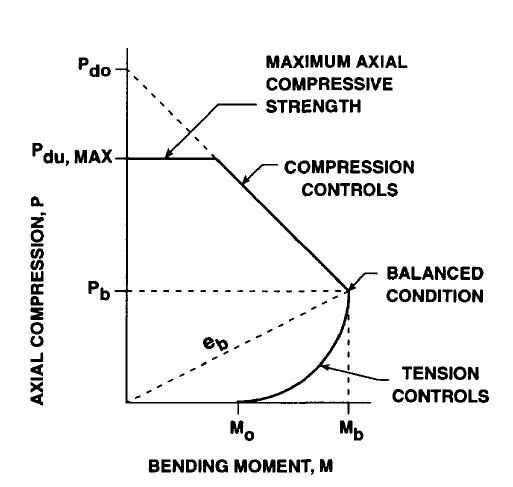
ככל שגדל הלחץ הצירי גדל מומנט התסבולת עד לנקודת מקסימום שמעבר לו קטן המומנט עד אשר הלחיצה דוקא גורמת להחלשת החתך.
באלמנט בטון מזוין, ככל שנגדיל את העומס הניצב לפני האלמנט, יגדל המומנט עד אשר יגיע לתסבולתו המקסימלית ואז יתחיל להתפתח פרק פלסטי. זה יכול לקרות כאשר הבטון יגיע למעיכה או עד אשר מוטות הזיון יגיעו למאמץ הכניעה (נזילה). בתכנון טוב ויעיל רצוי להגיע למצב בו הבטון יגיע לקצה גבול תסבולתו בלחיצה והפלדה תגיע לכניעה בעת ובעונה אחת. במקרה זה נקבל את המומנט המקסימלי בדיאגרמה לעיל. (נקודת האיזון)
לצורך הדגמה אחשב קיר נושא שגובהו 3 מ' ועוביו 30 ס"מ כאשר הברזל האנכי מורכב ממוטות מצולעים בקוטר 16 מ"מ בכל 10 ס"מ והמוטות האופקיים הינם בקוטר 12 מ"מ. רשתות אלה נמצאות משני צידי פני הקיר.
הקיר מחושב בסכימה של דו - רתום.
הקיר מחושב ל 4 מצבי לחיצה כדלקמן: 0 , 150 , 300 , 600 טון למ"א קיר.
עומס הפיצוץ (כמות חומר נפץ – מרחק ) הוא בהתאם לקריטריון פיקוד העורף.
ניתן לבצע את החישוב בשיטות כדלקמן:
חישוב "מקורב" אלסטי-פלסטי של מערכת בדרגת חופש אחת
מערכת של קפיץ מסה ומרסן המדמה את תגובת נקודה מרכזית בקיר או העמוד המייצגת את התנהגות האלמנט כולו.
לאחר קביעת הערכים המייצגים של הקשיחות, המסה (והריסון במידת הצורך), פותרים את משוואות התנועה של המערכת לקבלת הדפורמציות של המבנה.
השיטה היא די פשוטה ומקובלת מאד בתכנון מבני מגן. יחד עם זאת מדובר בשיטת חישוב מקורבת כאשר גם הריאקציות הדינמיות מחושבים בצורה מקורבת על ידי שילוב של הכפלת מקדמים בעומס הפיצוץ עם עומס התסבולת המקסימלית של האלמנט.
חישוב "מדויק" בעזרת תוכנת סימולציה באלמנטים סופיים
במקרה זה המבנה מחולק לאלמנטים סופיים כאשר אלמנטי הבטון ממודלים כאלמנטי "סוליד" ומוטות הפלדה כאלמנטי "קורה". ככל שנקטין את גודל האלמנטים, כך נקבל תוצאות מדויקות יותר מחד, ומאידך יגדל זמן החישוב.
תכונות החומרים כוללים את דיאגרמת מאמץ - עיבור של הבטון ומוטות הפלדה וכן את גרף של המקדם הדינמי המתאים לקצבי העיבור הגבוהים הקיימים בעומסי פיצוץ.
בשלב ראשון מעמיסים את המודל בכוח לחיצה צירי הגדל ליניארית במשך זמן מספיק ארוך (לפחות פעמיים זמן התנודה הטבעית של הקיר).
לאחר מכן מפעילים את עומס הדף הפיצוץ.
התוכנה מאפשרת לאחר גמר החישוב לקבל תוצאות של כל פרמטר החשוב לנו (הסטורית דפורמציות, מאמצים, עיבורים, כוחות גזירה דינמית וכיו"ב).
את הקיר חילקתי לאלמנטים קוביתיים בצלע של 10 מ"מ, את מוטות הזיון חילקתי גם כן לאורך של 10 מ"מ לכל אלמנט.
להלן מספר תוצאות של החישוב למצב של עומס לחיצה של 300 טון למ"א קיר. צורת הקיר במצב של דפורמציות מקסימליות (בתמונה הדפורמציות מוכפלות פי 10).

להלן הסטורית הדפורמציות של מרכז הקיר:
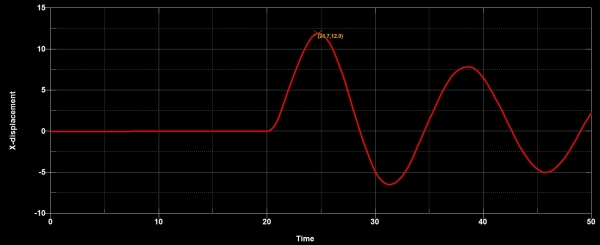
אנו רואים כי הקיר מתחיל להגיב רק אחרי 20 מילישניות מאחר ובזמן זה הקיר הועמס בלחיצה. השקיעה המקסימלית המתקבלת- 12 מ"מ.
בתרשים הבא נוכל לראות את הכוחות במוט הפלדה המרוחק מהחזית המועמסת בהדף.
בתרשים מופיעים הכוחות של 3 נקודות במרכז, בריתום ובנקודה אמצעית.
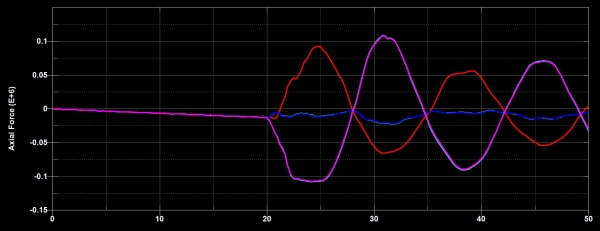
נראה כי מרכז המוט מתחיל במתיחה לאחר לחיצה קטנה הנובעת מהעמיסה בלחיצה.
המוט בקצה הרתום מתחיל בלחיצה בעוד הנקודה האמצעית נושאת כוחות לחיצה נמוכים לכל אורך החישוב. ניתן לראות מהתרשים כי מוט הזיון עבר את מאמץ הנזילה.
בתרשים הבא נראה את הסטורית כוחות הריאקציה הדינמית במרחק D מהסמך הרתום.
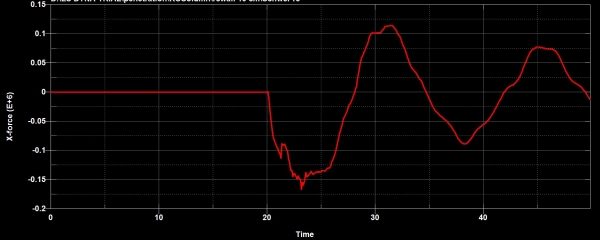
סיכום
לסיכום אשווה את התוצאות בשיטות החישוב השונות.
חישוב "מקורב" בתוכנת SBEDS, תוכנה שפותחה על ידי צבא ארה"ב ומבוססת על מערכת בדרגת חופש אחת. ניתן לחשב את הקיר כפלטה אבל במקרה זה עומס הלחיצה מתורגם לתוספת עומס אקויולנטית המספקת את אותו המומנט המתקבל מהכפלת עומס הלחיצה בדפורמציה. במקרה זה הגדלת הלחץ תגדיל את הדפורמציה המקסימלית.
ניתן בתוכנה לעיל גם לחשב את הקיר כ"קורת-עמוד", כאן כבר עומס הלחיצה גם מחזק את מומנט התסבולת של חתך הבטון המזוין.
חישוב "מדויק" בתכנת LS DYNA שהיא תכנת סימולציות ידועה ומוכרת.
להלן תוצאות חישוב של הקיר בשיטות השונות הן לדפורמציה המקסימלית והן לכוח הגזירה המקסימלי:
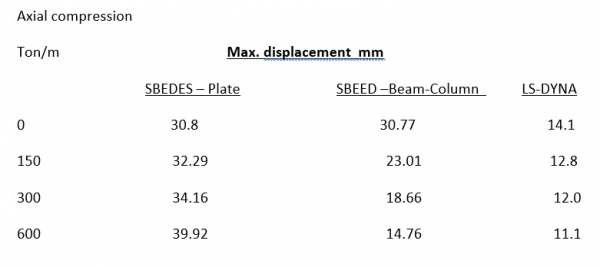

כפי שניתן לראות בבירור מהתוצאות:
- ככל שעומס הלחיצה גדל , הדפורמציות הצידיות קטנות (לא ככלל אלא רק לנתוני הבעיה שחושבה).
- הדפורמציות בחישוב ה"מדויק" קטנות מהדפורמציות המחושבות בחישוב ה"מקורב" (בשיטת מערכת מסה-קפיץ).
- הריאקציות הדינמיות המקסימליות גדולות בחישוב ה"מדויק" מאשר בחישוב ה"מקורב".
- למסקנה זאת יש משמעות חשובה בהערכת הסיכון לכשל בגזירה של האלמנט המחושב ומומלץ להמשיך ולחקור תופעה זאת.
למאמרים נוספים של אריה בוימל בנושא מיגון מבנים ורעידות אדמה:















אין תגובות