קביעת חוזקו של הבטון
מבוא
בפעם הראשונה הוצעה שיטה סטטיסטית לבדיקת חוזקו של הבטון במאמרי שפורסם בביטאון אגודת האינג`ינרים והארכיטקטים בישראל, מאי 1982, ואני מוצא לנכון לחזור על עיקרי הדברים והוכחת נחיצות השיטה לאור העובדה המצערת כי מאז דבר לא שונה, לא שופר, לא חודש. זה הזמן לגלות כי בזמנו דרבן אותי למחקר זה - פרופ` יצחק אלפן ז"ל, מהפקולטה להנדסה בנאית בטכניון, אשר למדתי בהדרכתו לימודי תואר שני בהנדסה אזרחית שהוסבו לאחר מכן לאפיק תכנוני אחר.
הצגת הבעיה
כאשר מוקם מבנה המצריך התחשבות בטיחותית בחוזק הבטון, קיימת בעייה של השגת בטון טוב שישביע את דרישות החוזק של המבנה מחד, ושל הכנת בטון לא "יותר מדי טוב" שלא לצורך.
כמו כן, קיימת בעיית ההחלטה לאחר היציקה, ולאחר קבלת תוצאות בדיקות הבטון על ידי מעבדה מאושרת, האם הבטון משביע רצון אם לאו. לולא התחשבות בבטיחות המבנה, היינו נגררים להכנת בטונים ירודים, בעלי חוזק ירוד, ובעיקר - זולים וקלים ליישום.
לולא התחשבות בגורם הכלכלי, היינו נגררים להכנת בטונים מעולים ביותר, בעלי הרכב אחיד לכל סוגי המבנים - הרכב האמור לספק בטון בעל חוזק מקסימאלי אפשרי, ללא כל תלות בחישובים הסטטיים.
במציאות עלינו לחפש את הדרך להכנת בטון חלש, שעדיין יהיה מספיק חזק כל שנוכל לקבוע בוודאות סבירה כי הוא מתאים לציפיותינו ועונה על דרישותינו.
רצוי לקבוע שיטות סטטיסטיות בדוקות לגבי פסילת בטון או אישורו, על מנת שלא נפסול בטון "טוב" ולא נאשר בטון "גרוע". התשובות צריכות להינתן כהצעת שיטה לשימוש המהנדסים העוסקים בתחום, אשר יוכלו להפעיל שיקול דעת עצמאי ולא להסתפק בתקן או בכל פורמט דוגמתי אחר - וזאת דווקא משום אחריות המהנדס על חוזק המבנים שהוא מתכנן, בהתאם לחוק המהנדסים והאדריכלים תשי"ח 1958 וותקנותיו, ובהתאם לחוק התכנון והבניה תשכ"ה - 1965 ותקנותיו.
בשלב מסוים של חישוב המבנה, יש להחליט החלטה בדבר החוזק הנדרש של הבטון. מן הדין שאותו מהנדס המחליט החלטה זו, הוא גם יקבע אחר כך - ורק הוא - האם יש לסווג את הבטון על סמך התוצאות של הבדיקות שנעשו, כמשביע רצון או לא.
ליקויים במצב הקיים
במדינת ישראל קיימים תקנים שעניינם חוזקו של הבטון, וביצוע בדיקות בנדון, ויש גם הוראות פנימיות של גופים שונים - הג"א, משרד הבינוי והשיכון, ועוד. עמידתו של הבטון בדרישות נעשית בהתאמה להוראות התקן הישראלי - ולא נתונות לשום שיקול דעת של המתכנן, דבר שהוא פסול לכשעצמו.
הנכון הוא, כי מהנדס צריך להציג חישוב לגבי חוזק הבטון לאחר קבלת תוצאות הבדיקה, כי חוזקו של הבטון הוא משתנה רציף אינסופי, והוא תלוי בממוצע האריתמטי שכל כך מקובל כקריטריון לחוזק הבטון - אולם הוא גם תלוי בגורמים אחרים, כגון: גודל המדגם [מספר הבדיקות], סטיית התקן [פיזור התוצאות של הבדיקות].
אנו לוקחים מדגם בגודל מסוים, ובודקים את חוזק הבטון של המדגם. רק אם ניקח מדגם בגודל אינסופי, כגודל האוכלוסייה האינסופית, נוכל לומר כי אכן החוזק הממוצע של המדגם הוא כחוזק הממוצע של האוכלוסייה, ובכל מקרה אחר - אין הדבר כך.
לשאלה מהו החוזק הממוצע של בטון ממנו נוטלים מדגם בן 3 קוביות בטון, שתוצאותיו הן כדלקמן: x1 x2 x3 והממוצע האריתמטי של בדיקות אלו יהיה Ā.
Ā = [x1+x2+x3]:3
אין תשובה חד משמעית ואין להסיק מהממוצע האריתמטי כאילו הוא החוזק הממוצע של הבטון שממנו נלקח מדגם.
כל מה שאפשר לומר הוא - כי יש הסתברות של p% שהחוזק של הבטון הנבדק הוא גדול מערך y, כאשר לכל ערך של pi ישנו ערך תואם של yi.
לאמור, יש לשאלה המודגשת בקו תחתון לעיל אינסוף תשובות, ולהלן כמה מהן:
א. ישנה הסתברות של 50% כי ממוצע חוזק הבטון עולה על הערך של הממוצע האריתמטי Ā
ב. ישנה הסתברות של 50% כי ממוצע חוזק הבטון קטן מהערך של הממוצע האריתמטי Ā
ג. ישנה הסתברות אינסופית כי ממוצע חוזק הבטון גדול מאפס.
ד. ישנה הסתברות אפס כי חוזק הבטון הוא אינסוף.
חשוב להבין את המצבים הללו כדי לדעת מהי התיאוריה העומדת מאחורי החישובים הסטטיסטיים שיובאו להלן.
אם המתכנן רוצה לדעת מהי ההסתברות שהבטון אשר ניטל ממנו מדגם ונבדק עונה בתכונות החוזק שלו על דרישות התכן, או במלים אחרות - מהו ממוצע חוזק הבטון בהסתברות של p%, מוצע מבחן השערה סטטיסטי כדי לקבל תשובה.
ברור כי דרישת חוזק ממוצעת להערכת חוזק הבטון לא מספיקה כקריטריון לקביעת חוזק הבטון. בתקן 118 [1] שכותרתו חוזק הבטון יש אומנם הגבלות בעניין חוזק נומינלי ["לא יעלה מספר המדגמים אשר חוזקם פחות מהחוזק הנומינלי, על שליש ממספר המדגמים שניטלו מאותו המבנה ושנבדקו באותו הגיל", ודרישות דומות], אולם אין דרישות גבוליות אלו למידת הפיזור של תוצאות המדגם מהוות מענה ישיר לשאלה שהוצבה לעיל. התלות כפי שהוצעה בעבר לראשונה על ידי י` סורוקה [2] - התקבלה ומצאה ביטויה בעדכוני התקן, אולם עדיין אין רצף בתלות בין קביעת חוזק הבטון לבין נתוני הבדיקה, וכל עוד אין רצף כזה, הבעיה אינה פתורה והסכנה היא באישור בטון גרוע כמו גם בפסילת בטון טוב.
על פי השיטה המוצעת להלן, המהנדס האחראי על שלד המבנה הוא ישלוט על ניתוח התוצאות ויהיה אחראי לכך, וחישוביו יהיו גלויים וברורים [למטרות: רישוי הבניה, בקורת על החלטותיו המקצועיות של המהנדס או חקירה במקרה של כשל].
לפי התקנים החלים כיום - המהנדס האחראי על שלד המבנה נמצא "מחוץ לתחום" של שיקול הדעת המקצועי, הנכנס לשבלונה תקנית, מחייבת, מהווה קריטריון להערכת חוזק הבטון – אך גם שגויה. השגיאה היא בכך שערכים האמורים להיות משתנים - הופכים באופן מלאכותי מאולץ להיות קבועים.
מאחר ובמציאות מתקבלים פיזורים שונים בבדיקות קוביות הבטון ללחיצה, ומאחר וברוב המקרים אין אנו יכולים להחליט מהן הסיבות למידת הפיזור, ומהי ההשפעה היחסית של כל גורם המשפיע על הפיזור, [סוג הבקרה, הדיוק המעבדתי, גורמים בלתי צפויים או בלתי ידועים], הרי חייבים להסיק על הפיזור לא באמצעות הנחות יסוד [המתאימות, אולי, למקרה שגרתי ממוצע], אלא על סמך תוצאות בדיקות המדגם ישירות.
לדוגמא: במקרה של תעבורת בטון המתבצעת בתנאי בקרה טובים, ולמרות זאת מתקבל פיזור רב - ההיגיון ההנדסי מחייב לא להתחשב בתנאי הבקרה הטובים, ולא להחליט על ערך גבוה יחסית של החוזק הממוצע של הבטון - וזאת מהטעם הברור שאותה בקרה אשר הגדרנו אותה כבקרה טובה - הוכחה כבקרה כלל לא טובה, וקיימת חובה חישובית להתחשב במידת הפיזור ולא בתנאי הבקרה הפורמאליים.
במלים אחרות: היחס בין החוזק הממוצע של הבטון לבין החוזק הנומינלי [חוזק הבטון לתכנון] צריך להינתן מתוך חישובים סטטיסטיים כתלות במידת הפיזור של תוצאות בדיקות המדגם, ולא כתלות בתנאי הבקרה הפורמאליים אליהם התכוונו מראש.
רק במקרה של התאמה בין הפיזור לבין סוג הבקרה - תעמוד שיטת התקן במבחן, והחישוב הסטטיסטי מיותר, אלא שמצב כזה מצוי בתיאוריה בלבד.
הצעה לפתרון, ודוגמאות חישוב
חוזקו של הבטון מפולג פילוג "t". את הפיזור בחוזק הבטון ניתן למדוד באמצעות סטיית התקן המדגמית "s", התלויה בגודל המדגם, בממוצע האריתמטי של תוצאות בדיקות המדגם ובהפרשים שבין הבדיקות לממוצע. פילוג "t" מתאים למדגמים קטנים הקטנים מ- 30, וידוע כ "Small Sampling Theory".
לגבי מדגמים כנ"ל, ההערכה של התקרבות גודל המדגם לאינסוף היא אינה מספיק טובה, ואי אפשר לאמץ את הנוסחאות המקורבות אשר בהן יש הזנחות הנובעות מביטול ההשפעה המתמטית של שאיפת גודל המדגם n לאינסוף. השיטה המדוייקת, המתייחסת למצב התיאורטי ידועה גם בכינוי Exact Sampling Theory"".
דוגמת מבחן השערה לוודאות בת 95%:
נניח שכתנאי מוקדם, יש דרישה כי 95% מהבטון יעלה על החוזק הנומינלי [p=0.95]. ההגבלה היא כמובן בכיוון אחד - אסור שיותר מ- 5% מהבטון יהיה נחות מתחת לערך 0µ אולם אין כל הגבלה לגבי אחוז הבטון מעל 95% שצריך להיות חזק מהערך של 0µ.
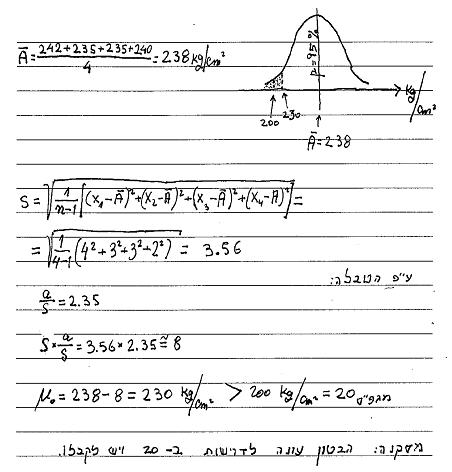
נדרש להכין בטון טוב כזה אשר 95% ממנו בעל חוזק של 200 ק"ג לסמ"ר. נבדקו 4 מדגמים בלחיצה, ולהלן התוצאות:
240, 235, 235, 242 ק"ג לסמ"ר.
בהנחה כי בטון טוב הוא כזה אשר 95% ממנו מעל חוזק של 200 ק"ג לסמ"ר ובטון גרוע הוא כזה אשר יותר מ- 5% ממנו הוא מתחת לחוזק הנ"ל, האם יש לקבל את היציקה או לדחותה?
פתרון:
ללא תלות בתנאי הבקרה, נחשב את הסטייה המדגמית s [ערך אקוויוולנטי לסטיית התקן במקרה של פילוג נורמאלי.
להלן החישוב בסיוע הטבלה שבסוף המאמר:
מבחן השערה לוודאות רצונית שאינה 95%:
לגבי אחוז כלשהו של בטון ירוד, α, מתקיימות הנוסחאות:
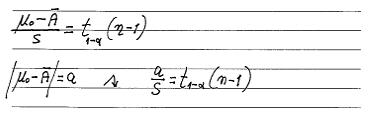
ניתן לערוך טבלה אשר בה יינתן הערך של a:s כפונקציה של α -1 ושל n.
דוגמת חישוב:
בהנחה כי בטון טוב הוא בטון אשר 70% ממנו מעל חוזק של 300 ק"ג לסמ"ר, דרוש לקבוע אם בטון הנותן תוצאות בדיקת קוביות בטון כדלקמן הוא אכן טוב, ואלו התוצאות בק"ג לסמ"ר: 250, 350, 450.
פתרון בסיוע הטבלה:

בדוגמא הנ"ל מסתבר כי למרות שהממוצע הוא 350 - גבוה בשיעור של 16.67% מהערך הדרוש, ולמרות שהמבחן הוא 70% בלבד - איננו יכולים לאשר את הבטון וזאת מחמת הפיזור הרב של התוצאות.
הערת שולים
עניין דומה ראה בשאלה ותשובה שלהלן: דוגמא להמחשת האבסורד המתמטי שבקביעת הממוצע כגורם משפיע: ראה בעניין זה מכתבו של המהנדס ב` יורוביץ אלי בשאלה מקצועית שהתפרסמה בבטאון אגודת האינג`ינרים והארכיטקטים בישראל גיליון 8-9/82 - להלן המכתב והתשובה כפי שפורסמו בשעתו, המהווים הבהרה מתמטית בנושא הנדון.
סיכום
לפרויקטים מסוימים ולאלמנטים קונסטרוקטיביים מסוימים, מתאימים קריטריונים שונים של רמת וודאות בדבר חוזק הבטון, והכללה בנדון - כפי שקיימת בספרות המקצועית ובתקנים - מעלימה מהמהנדס האחראי כלים חיוניים להחלטת החלטות מקצועיות לגבי הפרוייקט אותו הוא מתכנן ועליו הוא אחראי.
על כן, מוצע לעבור לשיטה סטטיסטית בקביעת חוזקו של הבטון כדי להגיע לקביעה מהימנה יותר של תוצאות, ותוך הישענות רבה יותר על אחריות המתכנן. בנוסף, השיטה המוצעת יותר מדויקת כי בה התלות בין המשתנים היא תלות רציפה כפי שהדבר במציאות, וללא מדרגות והנחות יסוד שאינן מתאימות למציאות.
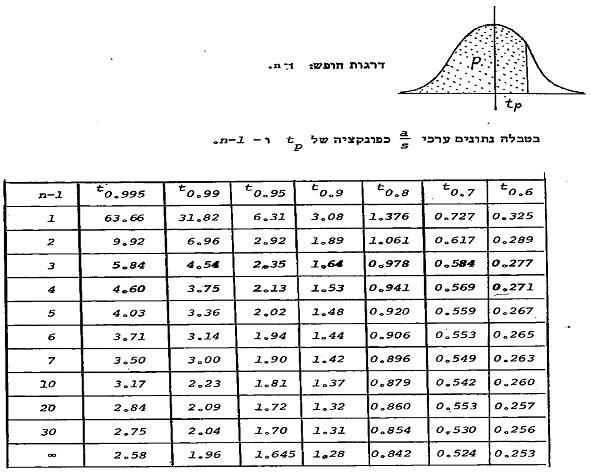
[הטבלה לקוחה מתוך מראה מקום מס` 6].
רשימת מראי מקום
[1] תקן ישראלי 118 - מכון התקנים הישראלי.
[2] "הערכה בקורתית והצעה לריביזיה של ת"י 118 - חוזק הבטון" מאת ד"ר י` סורוקה, "הנדסה ואדריכלות" מס` 1 1969.
[3] "קביעת חוזקו של הבטון" מאת א` בן עזרא, "הנדסה ואדריכלות" מס` 5 מאי 1982.
[4] מכתב ותשובה מתוך "הנדסה ואדריכלות" 8-9/82 דצמבר 1982.
[5] Theory and problems of statistics M. R. Spiegel, Schoum"s Aouthor series
[6] Statistical tabkes for biologicl; agrichultural and medical research [5th ed.]- R. A. Fisher and F. Yates, Table 3 Oliver and Boyd Ltd.
תגיות
הוספת תגובה
תגובות














אין תגובות